有限状态自动机

定义

FA是一个五元式

$$FA=(Q，\Sigma，\delta，q_0，F)$$

• $Q$ 是有限状态的集合

• $\Sigma$ 是字母表，即输入带上的字符集合

• $\delta$ 表示状态转移函数（$Q\times\Sigma\rarr Q$，即 $\delta(q, x)=q'$）代表 FA 在状态 $q$ 时，扫描字符 $x$ 后

  状态改变为 $q′$（也称到达状态 $q'$）

• $q_0$ 表示自动机的初态

• $F$ 表示自动机结束状态的集合

有限状态自动机的状态转换函数的个数应该为 $|Q|\times|\Sigma|$

对于Q中的每个状态，需要定义

对应∑每个字母的状态转换函数。

有向边的数目就是状态转换函数的个数。

DFA

对于不能接收的状态，应该要转换到一个特殊状态，陷阱状态

格局

格局是 DFA 某个瞬时状态的描述，格局发生变化是因为 $\delta$ 的一次作用。格局的转换如下：

停机

DFA 停机的情况是输入串扫描结束的时候，只有 这个时候才可以停机，不然就是陷阱状态。

DFA将输入串扫描结束停机时，如果DFA处于某一个接收状态， 则表示接收整个输入串；反之，则表示不接收整个输入串

NFA

扫描串w时，NFA的状态发生转换

可能会有三种情况：

• 可能在接收状态时终止；
• 可能在非接收状态时终止；
• 也可能在中途停止（中止）。

接收一个语言的步骤，做题步骤：

1. 给出该语言的正则表达式；
2. 构造 NFA 接受该语言；
3. 将 NFA 转换为等价的 DFA。

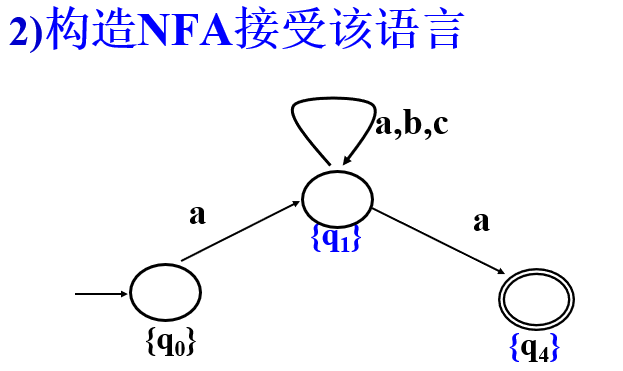
NFA 确定化

将 NFA 转换成 DFA，需要考虑每个状态的等价情况，结合所给出的语言的特点，将其状态转移函数不唯一的状态进行修改。确定化的方法参考本科学习的编译原理词法分析部分。

最终确定化后，每个状态的对应每个字母表中的字符只有对应的唯一一个状态，也就是 $\delta$ 函数唯一。

epsilon-NFA

能够接收 $\epsilon$ 的 NFA。对于 $\epsilon-NFA$ 需要确定其 $\epsilon-CLOSURE(x)$，表示经过 $\epsilon$ 后可以到达的状态集合，也就是要把这些 $\epsilon$ 的边消掉，做到变成 NFA。构造 NFA 也可以考虑每个状态的等价情况，目的是利用语言的特点消除掉空串。

$\epsilon-NFA$ 转 $NFA$ 的方法：

1. 求各个状态的 $\epsilon-CLOSURE(x)$，得到新的状态转移矩阵。
2. 消掉原来的 $\epsilon$

danger

要求构造 NFA 的时候也可以构造 DFA，因为 DFA 是特殊的 NFA。