KNN与线性分类器
Background
随着对于图像的研究,我们可以知道图象其实就是很多个数字组合到一起之后形成的矩阵。对于不同的物体,其表达都不相同。那么就很需要一个分类器,能够对这些图片进行区分。所以就提出了以下两种用于分类的数学模型。
计算机视觉的任务之一就是要从一堆数据当中识别出对应的类别,就像我们人类能够识别不同的物体,所以图像识别任务本质上就是图像分类问题。
但是,要想识别图像并不像识别一串数字那么简单。一串数字我们可以通过传统的算法来自动求解,得到想要的结果,可以通过编写一个程序的执行顺序来逻辑识别。但是图像不同,图像是一大堆宏观看起来毫无规律的数字,传统算法无法处理这些数据,发掘不了其内在特征。所以图像识别任务都是基于数据驱动的方法,通过收集数据,训练分类器,预测新的图片。
学习图像的分布规律,提取出图像当中的特征,最终实现识别。
KNN
KNN(第 k 最近邻算法),通过衡量两张图片的距离来比较图片的相似程度,根据距离最近的对图像数据进行分类。最常用的一般是 距离。
距离:
距离:
一般 距离比较普适, 距离一般用于具有一定语义的数据。
两张图片的距离越接近,说明越相似。使用 距离更加接近平滑的边界。点击此链接可进入 knn 可视化展示。
当 时,表示最近邻算法,表示数据集合中,待预测 的数据与类别 的数据距离最近,则 属于 这个类别。
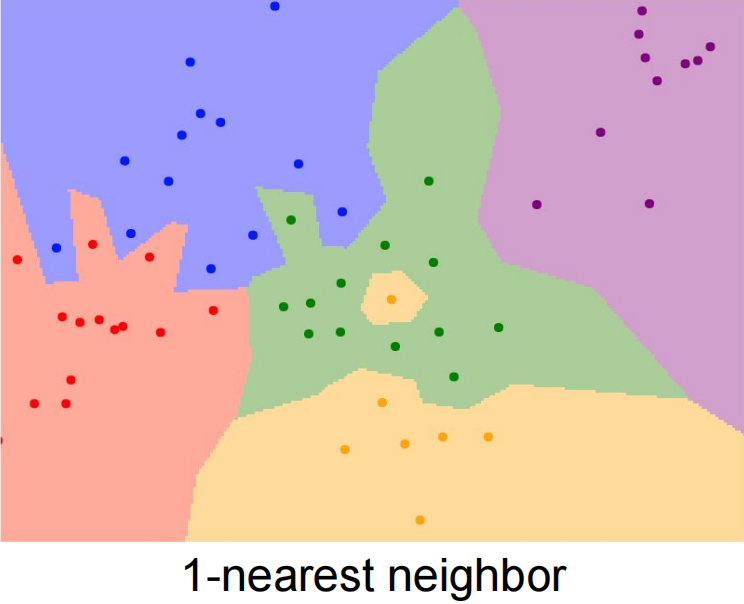
当 时,表示数据集合中,待预测数据 与类别为 的大于等于两个数据最近,则 属于 这个类别。
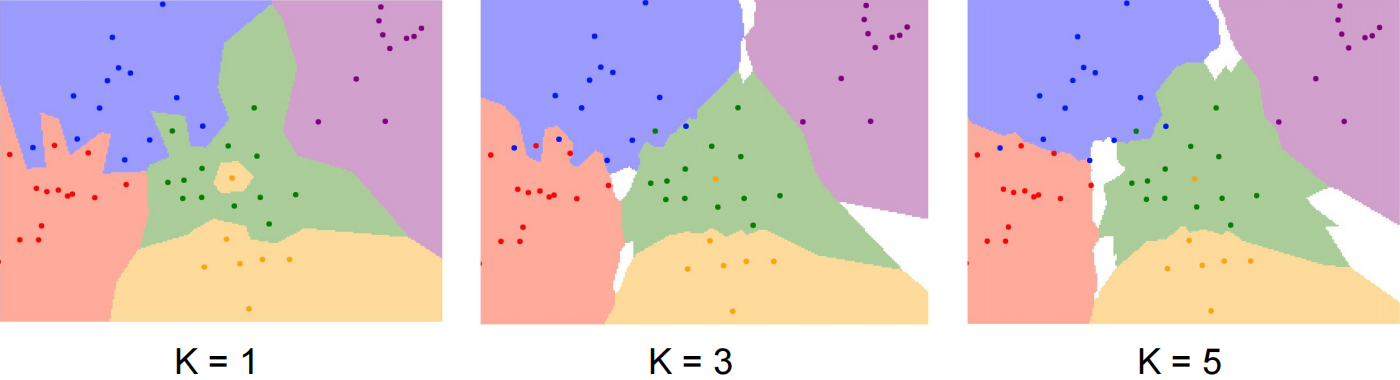
因为从客观规律上来看,与类型相同的数据在一起说明有较大的概率这个数据也是这个类别。
KNN 有两个超参数, 和 使用哪种距离指标()。
算法缺陷:
- 对于图像而言,不同图像质量各不相同,仅从距离这一角度来描述图像不够全面,过于宽泛,不能很好的区分各个类别。对于下面的图像使用距离就无法进行判断。

- 时间复杂度过高,对于三维数据,需要使用 的复杂度来计算,维度数越高复杂度越大。
数据集训练
有了数据 + 算法,我们就可以开始训练分类器的模型。对于每一次训练,数据集的划分是至关重要的,数据集划分的好坏决定了模型的好坏。
如果举例子来理解,最直观的是高考的例子,训练集就是我们平时学习训练的习题,通过练习来学会求解解题。验证集就是我们平时的模拟考试、期末考试等。测试集就是最终的高考试题。
那么平时做题训练的时候,有可能有的同学会死记硬背,就只记住这道题怎么写,下次换一下就不会了(过拟合)。有的同学是真的学会了做题,然后能应对考试中的题(拟合)。
从高考的角度而言,我们肯定是不希望出现只会死记硬背的同学,加入验证集就能够知道哪些同学是死记硬背的,然后反映出当前这次训练中到底也没有过拟合。如果出现了这样的情况我们能够及时知道并进行调整。但是平时测试终究还是测试,不是真正的高考。所以通过真正的高考能够真实反映模型的效果。
总结一下,划分这三个集合就是为了防止出现过拟合的现象,更好地反映训练过程中是否出现过拟合等情况,确保模型的泛化能力。测试集是我们人类都不能知道的,因为人这个因素会干扰模型的训练,当你觉得精度还可以提升时,往往继续训练就变成了过拟合。
数据集划分一般可以分为几种模式(这里针对分布在同一个数据集):
纯训练集( 训练集)
缺陷:只能完美地拟合训练集,无法检测出训练的效果。
训练集 + 测试集( 的训练集, 的测试集)
缺陷:只知道训练的效果,无法清楚对于新数据是否有效。
训练集 + 验证集 + 测试集
目前比较常用的方法。
训练集 + K 折交叉验证集 + 测试集
目前比较常用的方法。(数据量较小的情况下可用)
线性分类器
为了解决上述 KNN 描述问题,所以提出了一种基于参数的方法,通过线性函数来进行分类。因为线性函数能够很好地划分出类别,具有明显的特征性质。通过调节权重使得线性函数能够拟合某一个分布,使得这个线性函数能够划分出不同类别的数据。
线性分类器本质上就是线性函数,对于高维数据就是线性方程组。
以 Cifar10 数据集举例(10类别),对于一个 的数据,一般先对其进行向量化,转化成 的向量,作为自变量 ,表示整个图像上所有的像素,对于所有的像素需要有一个权重,所以构造一个 的权重矩阵,加上 的 bias 。最后计算为:
上述式子的含义为: 表示对于图像上每一个像素点都有一个权重,并且对于每一个类别都有一个权重。偏执 表示对于每一个类别的都有一个偏执 bias,最后得到的向量 表示输入的 对于每一个类别的分数,分数最高的就说明属于该类别。公式表示为:
假设上述表述用变量代替:
线性方程组表示为:
表示类别 的分数。
下面以一个仅包含 4 个像素的图片举例:
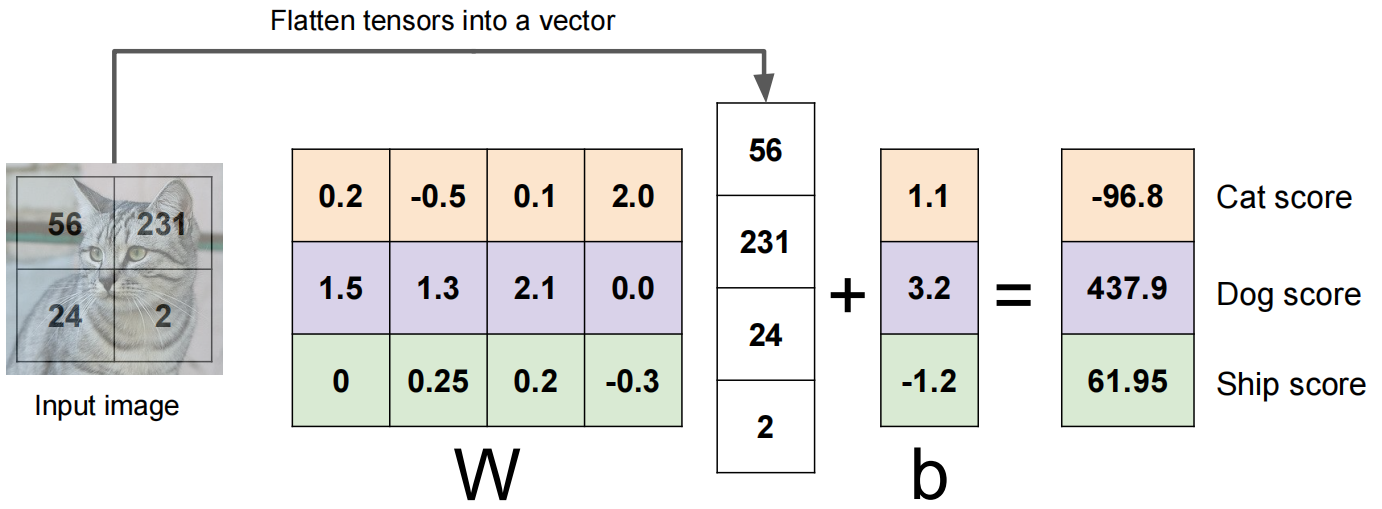
实际上,上述流程中,对于每一个类别都构建了一个线性分类器,一个线性分类器就对应一个高维向量的线性函数,对于不同类别就有不同的线性分类器。线性函数在 2d 上就表示一条直线,在 3d 上表示一个平面,超过 3d 上就表示为超平面。
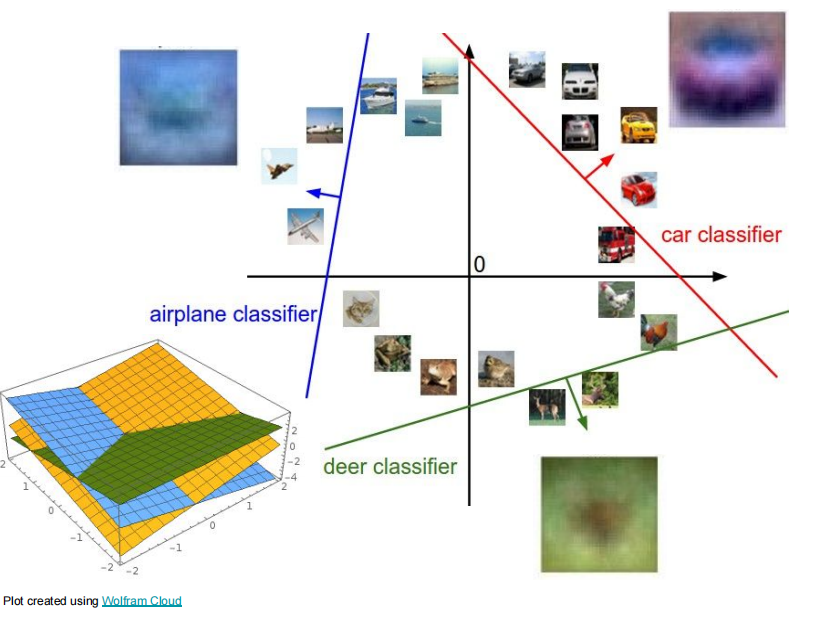
线性分类器的缺陷:
- 无法解决异或性质的问题,因为异或本身就是一个非线性的问题,无法用线性描述。异或的特点:相同为 0,不同为 1。
- 对于圆形分布数据无法用线性划分。
- 三种数据模式无法划分。
对于以上问题,其实本质上就是非线性问题无法用线性函数来分类,所以在之后的章节中会讲到如何使用非线性函数解决分类问题。
最近邻算法,衡量两个图像的距离,L1距离(曼哈顿距离)有语义可用
因为一个最近邻边界不够平滑,所以可以增加附近k个点的投票,跟类型相同的一起大概率这个人也是这个类型的。距离的衡量还有L2,比较普适,更加平滑。关注算法直觉。
调参
knn在图像上应用的问题
线性分类器其实就是一个直线(2d)、平面(3d)