Skip to main content

Neural Classifiers

Intro​

本节课的目标：

  1. 学会接触单词的词义
  2. 学习神经网络分类器的概念
  3. 能够顺场地看一些 word embedding 的论文，例如 Google word2vec 论文、GLoVe 论文等

Review​

上节课我们建立了如何构建 word vector 的模型，并且推导出如何求解和优化词向量模型，但这只是最简单的算法，这个算法能够比较好的学习单词之间的相似性和词义的方向，更好地预测周围的单词。

Bag of Word Model

Bag of Word，也就是 NLP 当中的词袋模型。其实我们的词向量本质上也是一种词袋模型，他不会关注单词所在的位置或者顺序，预测的概率是相同的。但这种模型也是非常粗糙的，不够精细。

word2vec 其实是将意思相近的单词在高维的向量空间当中彼此靠近，将相似的单词分组。

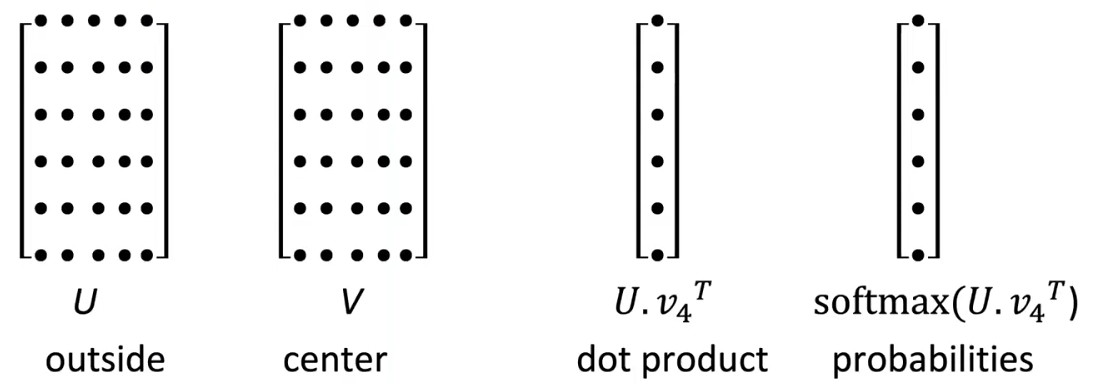
image-20221206111247762

通过 UU 和 VV 的点乘，经过 softmax 后得到相应单词的概率。而词袋模型是对每个位置的单词都做同样的 prediction 的操作，我们最终的目标是对于每个单词出现的预测的概率最大。

Word2Vec Optimization​

构建目标函数之后需要求解其最优概率，去找到目标函数的最值，所以使用梯度下降进行优化。

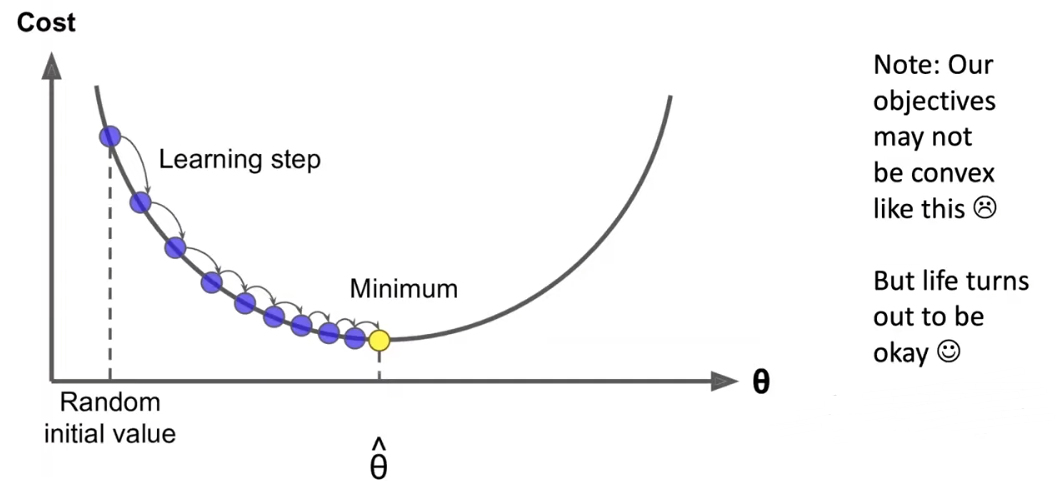
image-20221206152922620

梯度下降的核心思想是使用梯度来更新自变量，比较因变量之间的差距，通过不断更新自变量从而找到使得其函数达到最值的自变量的点。所以优化方式如下： for a matrix:

θnew=θold−α∇θJ(θ)\theta^{new}=\theta^{old}-\alpha\nabla_\theta J(\theta) \\

for a single parameter:

θjnew=θjold−α∂∂θjoldJ(θ)\theta_j^{new}=\theta_j^{old}-\alpha\frac{\partial}{\partial\theta_j^{old}}J(\theta)

但使用上面的方式会产生巨大的计算量，使得求得最值需要耗费长久的时间，所以提出 Stochastic Gradient Descent (SGD) 来优化，使用一批数据优化梯度下降的效率。

但是直接对 word vectors 使用梯度下降会产生一个问题，上下文间隔比较大的 word vector 可能概率值是很小的，所以就导致所计算的梯度矩阵是稀疏的（Sparse），从数学的角度上是合理的，但是从系统应用角度上这是不符合要求。

产生如下的稀疏矩阵：

∇θJt(θ)=[0⋮∇vlike⋮0∇uI⋮∇ulearning⋮]∈R2dV\nabla_{\theta}J_t(\theta)=\begin{bmatrix} 0 \\ \vdots \\ \nabla_{v_{like}} \\ \vdots \\ 0 \\ \nabla_{u_I} \\ \vdots \\ \nabla_{u_{learning}} \\ \vdots \end{bmatrix}\in \mathbb{R}^{2dV}

所以提出了如下解决方案：

  • We hope: 只更新真正出现在 word vectors 里面的参数
  • Solution:
    1. 只更新整个 embedding matrices U 和 V 中的确实存在有单词的那几行
    2. 给 word vectors 记录 Hash 值

Other Word2vec Algorithm​

为什么需要两个向量？→ 更容易优化。（但可以实现每个单词一个向量的算法）

对于 Word2vec 模型而言，还有一些变种的算法：

  1. Skip-grams (SG)

    根据 center word 预测 context words

  2. Continuous Bag of Words

    从 context words 预测 center words

提高训练效率的算法：

  1. Negative Sampling (naive softmax methods)

Skip-Gram Model with Negative Sampling​

因为使用传统的 softmax 方法的计算量非常大，因为要遍历每一个单词。 所以提出了 Negative Sampling 来优化计算。Negative Sampling 的核心思想是：训练一个 true pair (center word and a word in its context window) 与多个 noise pairs (the center word paired with a random word) 的二元逻辑回归模型。

info

This method is from paper called “Distributed Representations of Words and Phrases and their Compositionality” (Mikolov et al. 2013)

Main Idea

最终的目标函数如下：

J(θ)=1T∑t=1TJt(θ)σ(x)=11+e−xJt(θ)=log⁡σ(uoTvc)+∑i=1kEj∼P(w)[log⁡σ(−ujTvc)]J(\theta)=\frac{1}{T}\sum_{t=1}^TJ_t(\theta) \\ \sigma(x)=\frac{1}{1+e^{-x}} \\ J_t(\theta)=\log\sigma(u_o^Tv_c)+\sum_{i=1}^k\mathbb{E}_{j\sim P(w)}[\log\sigma(-u_j^Tv_c)]

sigmoid function will become your good friends!

通过最大化两个向量同时成立的概率最大，而 noise words 的概率最小，从而达到最优解。